Simulacija sudara u fizici
Uvodna prezentacija
(nakon nje slijedi 3D simulacija!)
Mauro Raguzin
Količina gibanja
$$\vec{p}=m\vec{v}$$
\(m\) — masa tijela
\(\vec{v}\) — brzina tijela
Veza količine gibanja i rezultantne sile čestice
$$\sum \vec{F}=\frac{d\vec{p}}{dt}=\frac{d(m\vec{v})}{dt}$$
- situacije gdje se vektor brzine mijenja s vremenom
- situacije gdje se masa čestice mijenja
- kada je rezultantna sila na česticu \(0\), vremenska derivacija količine gibanja je također \(0\) \(\Rightarrow\) količina gibanja je konstantna
ako je čestica izolirana, tada je nužno rezultanta \(0\) i \(\vec{p}\) je očuvan
Za slučaj s 2 čestice u izoliranom sustavu imamo \(\vec{F}_{21}+\vec{F}_{12}=\vec{0}\)
\(\Rightarrow\frac{d\vec{p_1}}{dt}+\frac{d\vec{p_2}}{dt}=\frac{d}{dt}(\vec{p_1}+\vec{p_2})=\vec{0}\)
Ovo vrijedi općenito, za svaku os pojedinačno u 3D i može se poopćiti na proizvoljan broj čestica u izoliranom sustavu
Zakon očuvanja količine gibanja
Ukupna količina gibanja izoliranog sustava konstantna je bez obzira na to kakvi se procesi i međudjelovanje događaju u sustavu
Jedan od najvažnijh zakona mehanike


Većina sudara u stvarnosti je negdje između

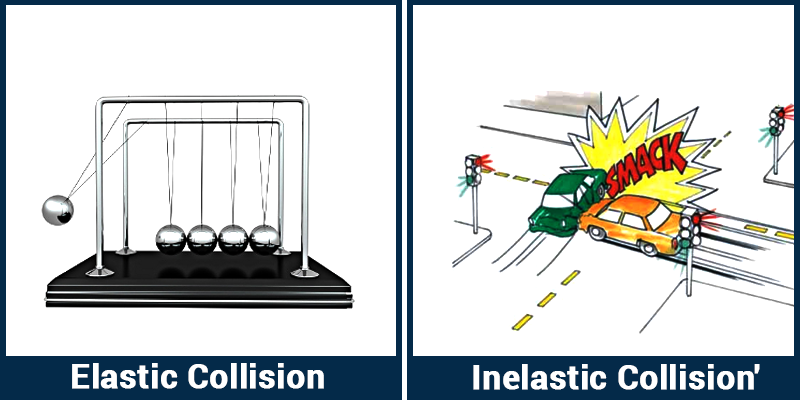
Savršeno neelastični sudari
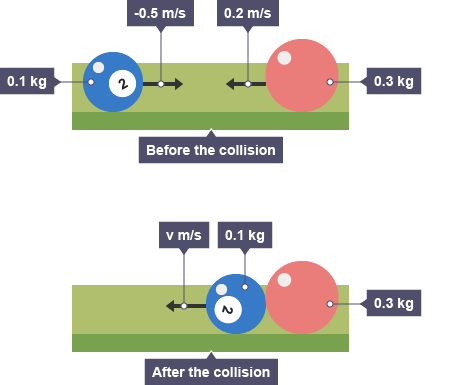
Dvije čestice se sudare i spoje zajedno u jedno tijelo te se nastavljaju gibati brzinom \(\vec{v_f}\)
$$v_f=\frac{m_1v_1+m_2v_2}{m_1+m_2}$$
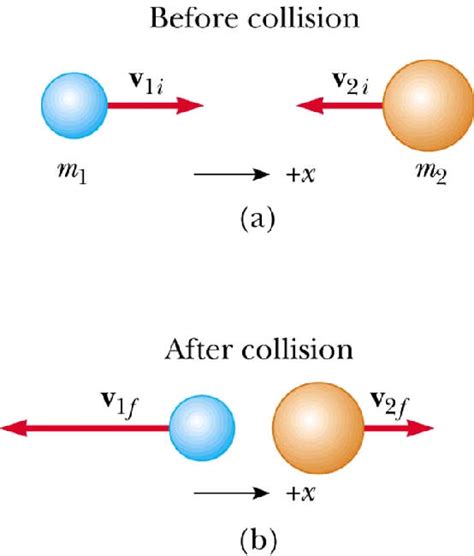
Elastični sudari
$$\begin{align*} v_{1f}&=\left(\frac{m_1-m_2}{m_1+m_2}\right)v_{1i}+\left(\frac{2m_2}{m_1+m_2}\right)v_{2i}\\ v_{2f}&=\left(\frac{2m_1}{m_1+m_2}\right)v_{1i}+\left(\frac{m_2-m_1}{m_1+m_2}\right)v_{2i} \end{align*}$$
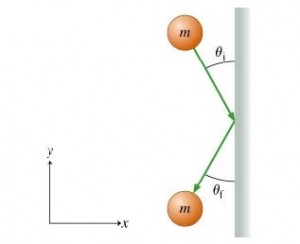
Posebni slučajevi:
- \(m_1=m_2=m\Rightarrow \vec{v}_{1f}=\vec{v}_{2i}, \vec{v}_{2f}=\vec{v}_{1i}\)
- \(m_1\ll m_2; \vec{v}_{2i}=\vec{0}\Rightarrow \vec{v}_{1f}=-\vec{v}_{1i}, \vec{v}_{2f}\approx\vec{v}_{2i}=0\)
- \(m_1\gg m_2; \vec{v}_{2i}=\vec{0}\Rightarrow \vec{v}_{1f}\approx \vec{v}_{1i}, \vec{v}_{2f}\approx 2\vec{v}_{1i}\)